4. Kansverdelingen
Binomiale verdeling
In het geval van n waarnemingen, alle onafhankelijk, elk resulterend in succes of mislukking, en elk met eenzelfde kans p op succes, spreekt men van een binomiale kansverdeling.
De kans op een bepaalde gebeurtenis kan men berekenen met de volgende formule:
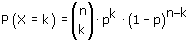
Zie uitleg formule
Het verwachting en de standaarddeviatie kan men berekenen met:
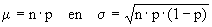
Voorbeeld
We gooien met 10 dobbelstenen. Wat is de kans op precies 3 keer een zes?
Invullen levert:
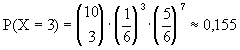
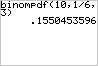
Met de GR
Met de GR kan dat sneller! Via [DISTR] (distribution=verdeling) en dan kiezen voor binompdf(. Dat staat voor 'Binomial probability distribution function'. De vraag is alleen even wat je precies als parameters moet opgeven. Wel aan...
Opgave 1
Een stochast X is binomiaal verdeeld met n=12, p=0,25.
- Bereken P(X=5)
De binomiale verdeling cumulatief
Op je GR staat ook nog binomcdf(, dat lijkt sprekend op de binomiale verdeling maar dan in plaats van p staat er een c. Die 'c' komt van 'binomial cumulative probability distribution function'.
Deze functie geeft de cumulatieve kans, dus bijvoorbeeld niet P(X=5), maar P(X
5).
P(X5) = P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5)
Anders geformuleerd:
...maar zo'n cumulatieve kans dat kan wel 's handig zijn...
Voorbeeld
Voor een tentamen algebra hebben zich 55 studenten ingeschreven. De docent heeft zich echter een beetje vertelt en heeft maar 50 toetsen gekopieerd. In het algemeen is bekend dat ongeveer 10% van de studenten die zich inschrijven voor een tentamen niet komt opdagen.
- Bereken op 3 decimalen nauwkeurig de kans dat er minimaal één toets overblijft.
Uitwerking
Dit is een binomiaal kansprobleem met n=55, p=0,9 (de kans dat een student komt opdagen) en er wordt gevraagd naar P(X49). Gelukkig... dat kan met de cumulatieve binomiale verdeling.
Opgave 2
Gebruik de gegevens van het voorbeeld hierboven.
- Bereken op 3 decimalen nauwkeurig de kans dat er meer dan 50 studenten op komen dagen.