3. Faculteiten, permutaties en combinaties

Onder [MATH] kan je van alles vinden. Bij bijvoorbeeld PRB (van probabilty=kans) kan je permutaties, combinaties en faculteiten vinden.

Permutaties
Als je k elementen kunt kiezen uit een verzameling van n elementen, waarbij ieder element hoogstens één maal gekozen wordt en waarbij wel gelet wordt op de volgorde van de elementen dan heb je te maken met een permutatie of rangschikking.
Het aantal permutaties kun je berekenen met de volgende formule:
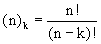
Je ziet in de formule de faculteiten staan, maar met de GR kan je dat sneller. Om (10)3 uit te rekenen toets je in je GR:
...en als het goed is komt daar dan 720 uit.
Combinaties
Als je k elementen kiest uit een verzameling van n elementen, waarbij ieder element hoogstens één maal wordt gekozen en waarbij niet gelet wordt op de volgorde dan heb je te maken met een combinatie.
Het aantal combinaties kan worden berekend met de volgende formule:
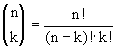
Je ziet hier ook weer faculteiten staan, maar met de GR kan je dat sneller. Om  uit te rekenen toets je in je GR:
uit te rekenen toets je in je GR:
..en als het goed is komt daar dan 120 uit.
Faculteiten
Met n verschillende elementen uit een verzameling van n elementen kunnen n! (spreek uit als n faculteit) verschillende permutaties (rangschikkingen) gemaakt worden. Men spreekt bij 'k uit n permutaties' ook wel van variaties en dan over permutaties bij 'n uit n rangschikkingen'. Maar tegenwoordig spreken we in beide gevallen over permutaties.
12! = 12·11·10·9·8·7·6·5·4·3·2·1 = 479.001.600
..en dat is al heel wat... dat betekent dat als je bijvoorbeeld 12 voorwerpen hebt je meer dan 470 miljoen verschillende volgordes kan maken... Hoe dat precies zit? Voor de eerste plaats kan je kiezen uit 12 mogelijke voorwerpen, voor de tweede plaats uit 11, enz. Dus in totaal op 12! manieren...
Opgave 1
Bereken met je rekenmachine:

Opgave 2
Op tafel staan 6 verschillende voorwerpen. Je kiest daar (zonder teruglegging) 3 voorwerpen uit.
- Op hoeveel manieren kan dat als de volgorde van belang is?
- Op hoeveel manieren kan dat als de volgorde niet van belang is?