6. Hellingsfunctie
Met behulp van het differentiequotiŽnt en een 'kleine stapgrootte' kan je bij elke functie een benadering van de hellingsfunctie of afgeleide vinden.
Voorbeeld
Voor een functie f geeft de volgende uitdrukking een benadering voor de hellingsfunctie:

Met de GR kan je dat gebruiken. Voor f heb ik f(x)=-0,1x3+2x-1 gekozen:


Y1 kan je vinden onder het [VARS] menu en dan kiezen voor [Y-VARS].
Dat levert in het grafiekenscherm toch een aardig plaatje op waar je veel kan ontdekken. Je kan bijvoorbeeld aan de nulpunten van de afgeleide zien waar de maxima en minima van f te vinden zijn. De raaklijn aan f is daar immers horizontaal... dus is de richtingscoŽfficiŽnt of helling in die punten gelijk aan nul.
Ook interessant is dat de afgeleide een maximum heeft. Wat betekent dat? In dat punt gaat toenemende stijging over in afnemende stijging. Voor de grafiek van f betekent dit dat je te maken hebt met een buigpunt.
Opgave 1
- Plot de afgeleide van f(x)=0,1∑(x-2)3-x. Bepaal met behulp van de nulpunten van de afgeleide de extremen van f.
- Plot de afgeleide van g(x)=0,01∑(x-2)5+x. Bepaal met behulp van het minimum van de afgeleide de coŲrdinaten van het buigpunt van g.
Opgave 2
- Plot de afgeleide van f(x)=ex. Wat valt je op?
Maar het kan nog mooier. In je GR is de 'benadering voor de afgeleide' al ingebouwd. De functie heet nDeriv(). Je kan het vinden onder [MATH]. Als je dan in Y1 een functie zet en je wilt de afgeleide en de tweede afgeleide plotten dan kan dat zo:
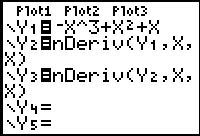
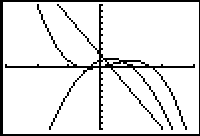
Je kunt de parameters van deze nDerive() zo zien:
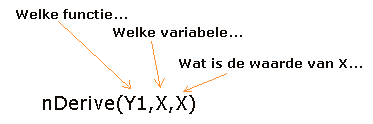
Als je de afgeleide wilt weten in een punt, bijvoorbeeld x=2 dan kan je nDerive() ook gebruiken vanuit het rekenscherm:

Opgave 3
- Gebruik nDeriv() om de eerste en de tweede afgeleide te plotten van f.
f(x)=sin(2x) en 0 x
x 2p en -5
2p en -5 y
y 5.
5.
Opgave 4
- Waar of niet waar: als de tweede afgeleide van een functie f nul is dan heeft f in dat punt een buigpunt.