|
Uitwerking
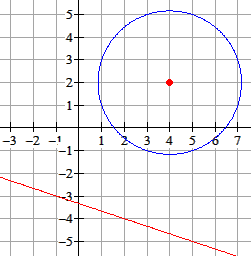
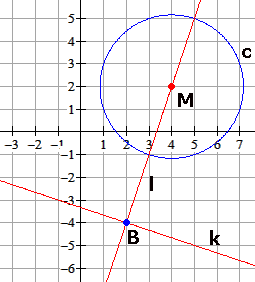
Bepaal eerst de coördinaten van het middelpunt $M$ van de cirkel.
$\eqalign{
& {x^2} + {y^2} - 8x - 4y + 10 = 0 \cr
& {x^2} - 8x + {y^2} - 4y + 10 = 0 \cr
& {(x - 4)^2} - 16 + {(y - 2)^2} - 4 + 10 = 0 \cr
& {(x - 4)^2} + {(y - 2)^2} = 10 \cr} $
De cirkel heeft als middelpunt $M(4,2)$ en $r=\sqrt{10}$.
Stel een vergelijking op van de lijn $l$ door $M$ loodrecht op $k$.
$\eqalign{
& x + 3y = - 10 \cr
& 3y = - x - 10 \cr
& y = - \frac{1}{3}x - 3\frac{1}{3} \cr
& r{c_l} = 3 \cr} $
De coördinaten van $M$ invullen in $y=3x+b$ geeft:
$l:y=3x-10$
Bereken de coördinaten van $B$: het snijpunt van $l$ met de lijn $k$.
$\begin{array}{l}
\left\{ \begin{array}{l}
y = - \frac{1}{3}x - 3\frac{1}{3}\\
y = 3x - 10
\end{array} \right.\\
...\\
\left\{ \begin{array}{l}
x = 2\\
y = - 4
\end{array} \right.
\end{array}$
$d(c,k)=d(B,M)-r=\sqrt{40}-\sqrt{10}=\sqrt{10}$
|