4. gelijkvormigheid
Vergroten en geiljkvormigheid
Bij gelijkvormige driehoeken:
- zijn de overeenkomstige hoeken gelijk
- passen de zijden van de driehoeken in een verhoudingstabel
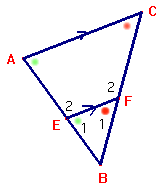
$
\eqalign{
& \Delta ABC \sim \Delta EBF }
$ betekent dat $\Delta ABC$ gelijkvormig is met $\Delta EBF$. Daarbij geldt:
- $\angle A=\angle E_1$ (F-hoeken)
- $\angle B = \angle B$ (triviaal)
- $\angle C = \angle F_1$ (F-hoeken)
Voorbeeld
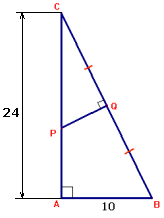
- Bereken de lengte van $AP$.
Uitwerking
- Bereken met de stelling van Pythagoras de lengte $BC=26$.
- $CQ=13$ (de helft van $BC$)
-
$\Delta ABC \sim \Delta QPC$
$\angle A=\angle Q$ (rechte hoek)
$\angle C=\angle C$ (triviaal)
$\angle B=\angle P$ (som van de hoeken) - Maak een verhoudingstabel
- Bereken $PC$ met kruislings vermenigvuldigen.
- $PC=14\frac{1}{12}$
- $AP=9\frac{11}{12}$