5. vergelijkingen van vlakken
De vergelijking en de normaalvector van een vlak
In het platte vlak heb je de assenvergelijking van een lijn. In de ruimte heb je een assenvergelijking voor een vlak.
Een assenvergelijking van het vlak $V$ door de punten
$P(p,0,0)$, $Q(0,q,0)$ en $R(0,0,r)$ is:
$V$:$\Large\frac{x}{p}+\frac{y}{q}+\frac{z}{r}$=$1$
Een normaalvector van een vlak $V$ is een vector (ongelijk aan de nulvector) die loodrecht op $V$ staat.
De vector $
\underline n _V = \left( {\begin{array}{*{20}c}
a\\
b\\
c\\
\end{array}} \right)
$ is normaalvector van het vlak:
$V:ax+by+cz=d$
Voorbeeld 1
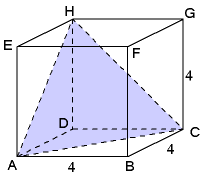
$
V:\frac{x}{4} + \frac{y}{4} + \frac{z}{4} = 1
$
$
V:x + y + z = 4
$
$
\underline n _V = \left( {\begin{array}{*{20}c}
1\\
1\\
1\\
\end{array}} \right) = \overrightarrow {DF}
$
Het uitproduct van twee vectoren
Het uitproduct van de vectoren
$
\underline a = \left( {\begin{array}{*{20}c}
{a_1 }\\
{a_2 }\\
{a_3 }\\
\end{array}} \right)
$ en $
\underline b = \left( {\begin{array}{*{20}c}
{b_1 }\\
{b_2 }\\
{b_3 }\\
\end{array}} \right)
$ is:
$
\underline a\times\underline b = \left( {\begin{array}{*{20}c}
{a_2 b_3 - a_3 b_2 }\\
{a_3 b_1 - a_1 b_3 }\\
{a_1 b_2 - a_2 b_1 }\\
\end{array}} \right)
$
De vector $\underline a\times\underline b$ staat loodrecht op $\underline a$ en $\underline b$
Voorbeeld 2
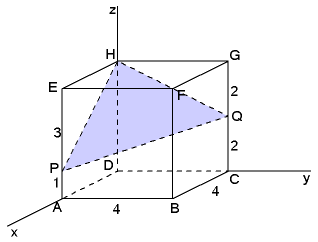
- Stel een vectorvoorstelling op van de lijn $k$ door het punt $C$ die loodrecht staat op het vlak $PQH$.
Zie uitwerking
Het uitproduct en een vergelijking van een vlak
Een richtingsvector van het vlak $V$ is een vector (ongelijk aan de nulvector) die in $V$ ligt of evenwijdig is met $V$
Voorbeeld 3

- Stel een vergelijking op voor het vlak $PQH$
Uitwerking van voorbeeld 3
Bij de uitwerking van voorbeeld 2 hadden de normaalvector van het vlak $V$ al gevonden:
$
\underline n _V = \left( {\begin{array}{*{20}c}
3\\
2\\
4\\
\end{array}} \right)
$
De vergelijking wordt dan:
$V:3x+2y+4z=d$
Vul een punt in om $d$ te berekenen en je bent er...
$V:3x+2y+4z=16$