domein en bereik bepalen van een wortelfunctie
$f(x)=\sqrt{x}$ is een standaardfunctie met $D_f=[0,\to>\,\,en\,\,B_f=[0,\to>$
De functie
$
f(x)=2\sqrt{x-3}+4
$
kan je opvatten als een
transformatie
van de standaardfunctie.
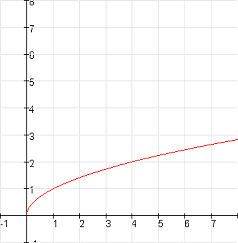
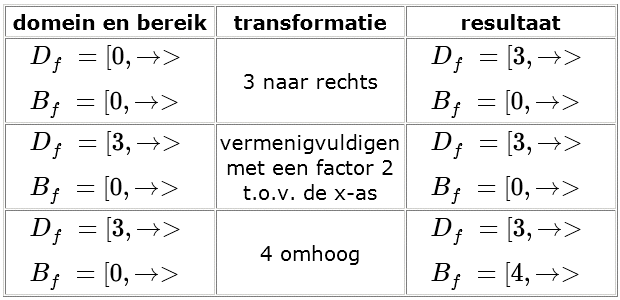
3 naar rechts verschuiven van
$x \to \sqrt{x}$
geeft
$x \to \sqrt{x-3}$
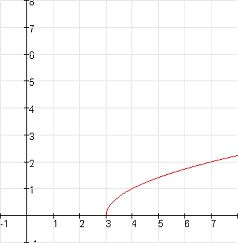
vermenigvuldigen van
$x \to \sqrt{x-3}$
met een factor 2 t.o.v. de x-as geeft
$x\to 2\sqrt{x-3}$
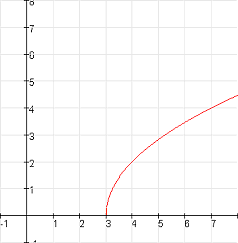
4 omhoog verschuiven van
$x\to 2\sqrt{x-3}$
geeft
$x\to 2\sqrt{x-3}+4$
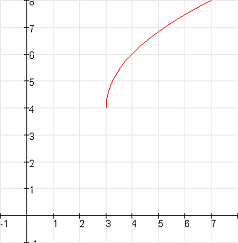
Conclusie
In de praktijk komt het domein en bereik bepalen van een wortelfunctie neer op:
- Bepaal het startpunt.
- Loopt de grafiek naar links of naar rechts?
- Loopt de grafiek omhoog of omlaag?
Als je dat weet dan weet je hoe 't zit...![]()