uitwerking A13
Het bad loopt leeg
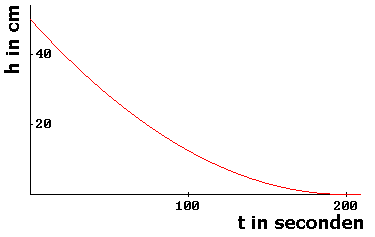
Bij het leeglopen van een bad loopt het water in het begin sneller weg dan aan het eind. Men gebruikt hierbij het model met een formule van de vorm:
$h=a(t-p)^2$
Hierin in $t$ de tijd in seconden en $h$ de hoogte in cm van het water in het bad.
In het begin staat het water 50 cm hoog en het duurt 200 seconden voordat het bad leeg is.
- Bereken algebraisch de snelheid waarmee de hoogte verandert op het moment dat het water 32 cm hoog staat.
Uitwerking
Met de punten $(0,50)$ en $(200,0)$ kan je waarden van $a$ en $p$ uit de formule bepalen.
$\begin{array}{l}
\left\{ \begin{array}{l}
50 = a{\left( {0 - p} \right)^2}\\
0 = a{\left( {200 - p} \right)^2}
\end{array} \right.\\
\left\{ \begin{array}{l}
50 = a{p^2}\\
a = 0\,\,(v.n.)\, \vee p = 200
\end{array} \right.\\
\left\{ \begin{array}{l}
50 = a \cdot {200^2}\\
p = 200
\end{array} \right.\\
\left\{ \begin{array}{l}
a = \frac{1}{{800}}\\
p = 200
\end{array} \right.\\
h = \frac{1}{{800}}{\left( {t - 200} \right)^2}
\end{array}$
De vraag is nu wat de waarde van $t$ is al het water op $32$ cm hoogte staat:
$\eqalign{
& \frac{1}{{800}}{\left( {t - 200} \right)^2} = 32 \cr
& {\left( {t - 200} \right)^2} = 25600 \cr
& t - 200 = - 160 \vee t - 200 = 160 \cr
& t = 40 \vee t = 360\,\,\,(v.n.) \cr
& t = 40 \cr} $
Met de afgeleide kan je dan de snelheid berekenen op $t=40$.
$\eqalign{
& h = \frac{1}{{800}}{\left( {t - 200} \right)^2} \cr
& h' = \frac{1}{{800}} \cdot 2\left( {t - 200} \right) \cdot 1 = \frac{1}{{400}}\left( {t - 200} \right) \cr
& h'(40) = - 0,4 \cr} $
De hoogte neemt af met $0,4$ cm/s.