Uitwerking van de opdracht
Opdracht
Los de vergelijking $x^3+16x=64$ op met behulp van Khayyam
Constructie
Het gaat om de vergelijking $x^3+16x=64$. Stel vast dat:
- $a=4$
- $b=64$
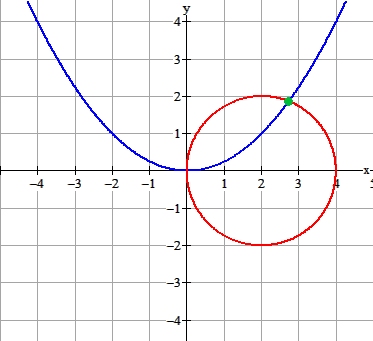
- $x^2=4y$
- $(x-2)^2+y^2=4$
- Snijden geeft $x\approx2,8$
Bewijs
Neem $y=\frac{}{}x^2$. Je krijgt dan:
$
\eqalign{
& (x - 2)^2 + \left( {\frac{1}
{4}x^2 } \right)^2 = 4 \cr
& x^2 - 4x + 4 + \frac{1}
{{16}}x^4 = 4 \cr
& \frac{1}
{{16}}x^4 + x^2 - 4x = 0 \cr
& x^4 + 16x^2 - 64x = 0 \cr
& x(x^3 + 16x - 64) = 0 \cr
& x = 0 \vee x^3 + 16x - 64 = 0 \cr
& x = 0 \vee x^3 + 16x = 64 \cr}
$
Er zijn nog meer typen vergelijkingen en er was nog ergens een ruimtelijke voorstelling. Deze constructies hebben te meken met kegelsneden. Dat ligt wel een beetje voor de hand.... cirkel (=kegelsnede) en parabool... Zijn het niveaukrommen? Of is hier iets anders aan de hand?