voorbeeld met uitwerking
Opgave
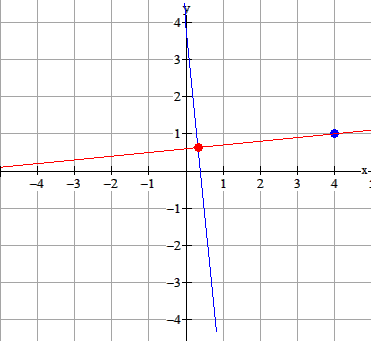
Gegeven de vergelijking van de lijn l:y=−10 x+4 en punt P(4,1).
- Wat is de afstand van punt P tot de lijn l?
Uitkwerking
De lijn $k$ loodrecht op $l$ heeft als vergelijking $y=\frac{1}{10}x+b$. Vul het punt $P(4,1)$ in en berekenen $b$:
$1=\frac{1}{10}·4+b$
$b=\frac{3}{5}$
Snijpunt van $l$ en $k$ bepalen:
$k:y=\frac{1}{10}x+\frac{3}{5}$
$l:y=−10 x+4$
$S:(\frac{34}{101},\frac{64}{101})$
Invullen:
$
d\left( {P,l} \right) = d\left( {P,S} \right) = \sqrt {(4 - \frac{{34}}{{101}})^2 + \left( {1 - \frac{{64}}{{101}}} \right)^2 } \approx 4,352
$
Helpt dat?
Naschrift