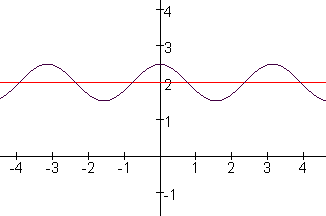
voorbeeld 2
Geef aan hoe de grafieken van de volgende functies uit een standaardgrafiek ontstaan en geef de evenwichtsstand, de amplitude, de periode en de coördinaten van het beginpunt.
$g(x) = 2-{\textstyle{1\over 2}}\cos (2(x+{\textstyle{1\over 2}}{\rm{\pi}}))$
Uitwerking
$y=\cos\left(x\right)$
Vermenigvuldigen met $\frac{1}{2}$ t.o.v. de $y$-as.
$y=\cos\left({2x}\right)$
Verschuif $\frac{1}{2}\pi$ naar links.
$y=\cos\left({2\left({x+\frac{1}{2}\pi}\right)}\right)$
Vermenigvuldig met $-\frac{1}{2}$ t.o.v. de $x$-as.
$y=-\frac{1}{2}\cos\left({2\left({x+\frac{1}{2}\pi}\right)}\right)$
Verschuif $2$ omhoog.
$y=2-\frac{1}{2}\cos\left({2\left({x+\frac{1}{2}\pi}\right)}\right)$
De evenwichtsstand is 2, de amplitude is $\frac{1}{2}$, de periode is $\pi$ en de coördinaten van het beginpunt zijn $(-\pi,2\frac{1}{2})$ of ook $(0,2\frac{1}{2})$.