|
De assenvergelijking van een lijn
De lijn door de punten $(a,0)$ en $(0,b)$ heeft de vergelijking $\eqalign{\frac{x}{a}+\frac{y}{b}=1}$ met $a\ne0$ en $b\ne0$.
Voorbeeld
De lijn $l$ gaat door de punten $(4,0)$ en $(0,-5)$. Geef een vergelijking voor de lijn $l$.
Uitwerking
Invullen geeft $\eqalign{\frac{x}{4}+\frac{y}{-5}=1}$. Vermenigvuldigen met 20 geeft:

|
De hoek tussen twee lijnen
De richtingshoek van een lijn is de hoek die de lijn maakt met het positieve deel van de $x$-as.
Voor de richtingshoek $\alpha$ van de lijn $k$ geldt:
-
$\tan\alpha=rc_k$
-
$-90^\circ\lt\alpha\le90^\circ$
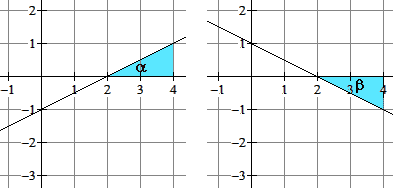
Voor de hoek $\varphi$ tussen twee lijnen met richtingshoeken $\alpha$ en $\beta$, waarbij $\alpha\gt\beta$, geldt:
-
$\varphi=\alpha-\beta$ als $\alpha-\beta\le90^\circ$
-
$\varphi=180^\circ-(\alpha-\beta)$ als $\alpha-\beta\gt90^\circ$
|
|
De hoek tussen twee krommen
De hoek tussen twee krommen in een snijpunt $A$ is gelijk aan de hoek tussen de raaklijnen in $A$.
Voorbeeld
Bereken in graden nauwkeurig de hoek waaronder de grafieken van $f(x)=\sqrt{x}$ en $g(x)=-2x+6$ elkaar snijden.
|
Voorbeeld
-
Bereken op 1 decimaal nauwkeurig de hoek tussen de lijnen $k:3x-2y=5$ en $l:4x-3y=6$.
Zie uitgewerkt 2

|