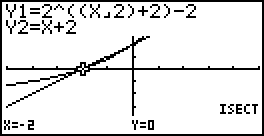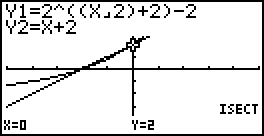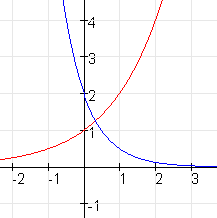
3. exponentiële functies

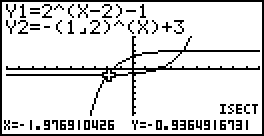
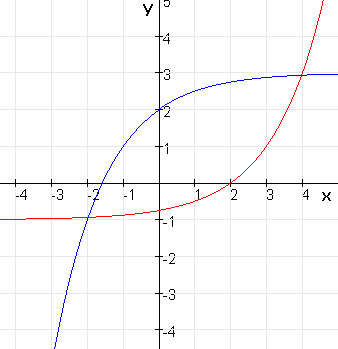
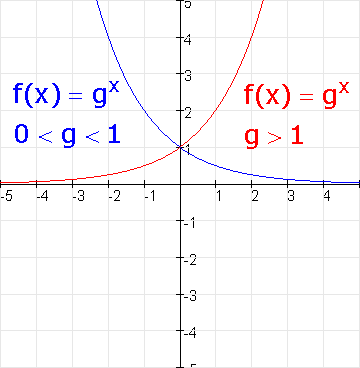
De standaardfunctie y=gx Een functie van de vorm $f(x)=g^x$ met $g$ constant en $g\gt0$ is een exponentiële functie. De variabele $x$ staan in de exponent. De grafiek van $f$ is stijgend als $g\gt1$ en de grafiek is dalend in het geval $0\lt g\lt1$. De $x$-as is een asymptoot. $D_f=R$ $B_f=<0,\to>$ De functie $f(x)=g^x$ is een standaardfunctie en de grafiek is een standaardgrafiek. Je mag ze zonder toelichting tekenen.

Transformaties en exponentiële functies Door de standaardgrafiek $y=g^x$ te verschuiven, te vermenigvuldigen of te spiegelen onstaan andere grafieken. Mogelijke transformaties: Spiegelen in de $x$- of $y$-as Verticale of horizontale verschuiving Vermenigvuldigen t.o.v. de $x$- of $y$-as Zie overzicht transformaties van grafieken voor een volledig overzicht. Voorbeelden Opgave $A50$ op bladzijde 32 Uitwerkingen Zie uitwerkingenboek Zie ook toepassingen van transformaties van grafieken

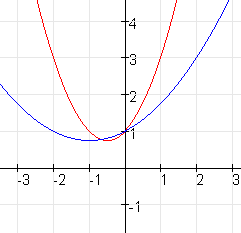
Vermenigvuldigen met een factor t.o.v. y-as Vervang 'x' door '$\frac{1}{a}$x' als je wilt vermenigvuldigen met de factor 'a' t.o.v. de y-as. Voorbeeld Als je $f(x)=x^2+x+1$ bijvoorbeeld wilt vermenigvuldigen met de factor $2$ t.o.v. de $y$-as dan krijg je: $f(x)=(\frac{1}{2}x)^2+\frac{1}{2}x+1$ $f(x)=\frac{1}{4}x^2+\frac{1}{2}x+1$

Exponentiële ongelijkheden

Voorbeeld 1 Los op: $2^{x-2}-1<-\left({\frac{1}{2}}\right)^x+3$ Uitwerking Neem $f(x)=2^{x-2}-1\,\,$. Neem $\,\,g(x)=-\left( {\frac{1}{2}}\right)^x+3$. Plot de grafieken op je GR, benader de snijpunten en geef de oplossingen zodat f(x)$<$g(x). Oplossing: -2,0$<$x$<$4,0
Voorbeeld 2 Gegeven $f(x)=2^{\frac{x}{2}+2}-2\,\,$en$\,\,g(x)=x+2$. Los op: f(x)>g(x) Uitwerking Benader de snijpunten met je GR. Oplossing: $x<2\vee x>0$ Is dit een exacte oplossing? Kun je de vergelijking f(x)=g(x) algebraïsch oplossen?
Voorbeeld 3 Los exact op: $4\cdot2^{x-2}<2\cdot\left({\frac{1}{4}}\right)^x$ Uitwerking Plot de grafieken met je GR en bereken exact het spijpunt. $ \eqalign{   & 4 \cdot 2^{x - 2}  = 2 \cdot \left( {\frac{1} {4}} \right)^x   \cr   & 2^2  \cdot 2^{x - 2}  = 2 \cdot \left( {\frac{1} {{2^2 }}} \right)^x   \cr   & 2^x  = 2 \cdot \left( {2^{ - 2} } \right)^x   \cr   & 2^x  = 2^1  \cdot 2^{ - 2x}   \cr   & 2^x  = 2^{ - 2x + 1}   \cr   & x =  - 2x + 1  \cr   & 3x = 1  \cr   & x = \frac{1} {3} \cr} $ Oplossing: $x>\frac{1}{3}$

Exponentiële vergelijkingen algebraïsch oplossen Sommige exponentiële vergelijkingen moet je algebraische kunnen oplossen. Voorbeelden $2^{x-3}=\sqrt{2}$ $3^{x+1}=\frac{1}{9}\sqrt{3}$ $2·3^{2x-1}=18$ Je werkt dan toe naar een vorm waarin het linkerlid en het rechterlid als macht van hetzelfde grondtal geschreven zijn. Je gebruikt: Als $g^A=g^B$ dan $A=B$

Voorbeelden $ \eqalign{   & 2^{x - 3}  = \sqrt 2   \cr   & 2^{x - 3}  = 2^{\frac{1} {2}}   \cr   & x - 3 = \frac{1} {2}  \cr   & x = 3\frac{1} {2} \cr} $ $ \eqalign{   & 3^{x + 1}  = \frac{1} {9}\sqrt 3   \cr   & 3^{x + 1}  = 3^{ - 2}  \cdot 3^{\frac{1} {2}}   \cr   & 3^{x + 1}  = 3^{ - 1\frac{1} {2}}   \cr   & x + 1 =  - 1\frac{1} {2}  \cr   & x =  - 2\frac{1} {2} \cr} $ $ \eqalign{   & 2 \cdot 3^{2x - 1}  = 18  \cr   & 3^{2x - 1}  = 9  \cr   & 3^{2x - 1}  = 3^2   \cr   & 2x - 1 = 2  \cr   & 2x = 3  \cr   & x = 1\frac{1} {2} \cr} $

• twee voorbeelden

©2004-2025 W.v.Ravenstein