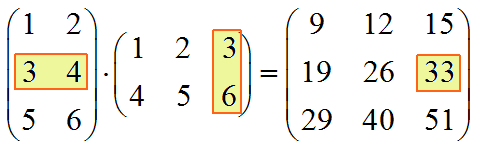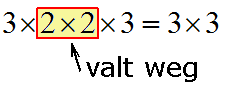|
Bewerkingen met matrices
Wat is een matrix?
Definitie
-
Een matrix is een rij reële getallen die gerangschikt zijn in rijen en kolommen.
-
Om aan te geven dat er sprake is van een matrix worden de tekens [ en ] of ( en ) gebruikt...
-
Als $m$ het aantal rijen en $n$ het aantal kolommen is spreekt men van een $m$x$n$-matrix of ook van een $(m,n)$-matrix.
-
Is $m=n$, dan is er sprake van een vierkante matrix. Het aantal rijen (of kolommen) heet dan de orde van de vierkante matrix.
-
Een kolom van een matrix wordt ook wel kolomvector; een rij van een matrix heet ook wel rijvector.
-
De $(p,q)$- en de $(m,n)$-matrix zijn van hetzelfde type (of van dezelfde vorm) als $p=m$ en $q=n$.
BRON: http://www.pandd.demon.nl/matrices.htm
Wat is een graaf?
Een graaf bestaat uit punten waarvan er twee of meer verbonden zijn door wegen.
Er bestaan verschillende soorten grafen met verschillende bijbehorende matrices.
De som van twee matrices
Twee matrices met dezelfde afmeting kun je optellen. De sommatrix krijg je door de getallen op de overeenkomstige plaatsen op te tellen.
\(\left({\begin{array}{*{20}c}1&2\\{-8}&3\\{-2}&4\\\end{array}}\right)+\left({\begin{array}{*{20}c}1&3\\0&3\\2&{-3}\\\end{array}}\right)=\left({\begin{array}{*{20}c}2&5\\{-8}&6\\0&1\\\end{array}}\right)\)
Vermenigvuldigen met een getal
Je kunt een matrix met een getal vermenigvuldigen. Je vermenigvuldigt dan elk element van de matrix met dat getal.
$2\cdot\left({\begin{array}{*{20}c}2&5\\{-8}&6\\0&1\\\end{array}}\right)=\left({\begin{array}{*{20}c}4&{10}\\{-16}&{12}\\0&2\\\end{array}}\right)$
Een matrix vermenigvuldigen met een kolommatrix
Je kunt een matrix $A$ vermenigvuldigen met een kolommatrix $K$ als het aantal kolommen van $A$ gelijk is aan het aantal rijen van $K$.
Als $A$ een 2x3-matrix en $K$ een 3x1-matrix is dan is de productmatrix $A·K$ een 2x1-matrix.
$\left({\begin{array}{*{20}c}1&2&3\\4&5&6\\\end{array}}\right)\cdot\left({\begin{array}{*{20}c}1\\2\\3\\\end{array}}\right)=\left({\begin{array}{*{20}c}{14}\\{32}\\\end{array}}\right)$
|
Het vermenigvuldigen van matrices
Twee matrices vermenigvuldig je door steeds een rij van de eerste matrix met een kolom van de tweede matrix te vermenigvuldigen.
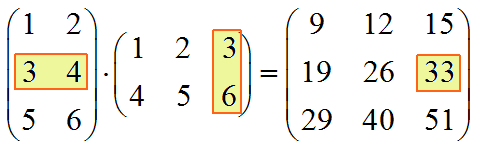
3 · 3 + 4 · 6 = 33
Daaruit volgt dat om twee matrices te kunnen vermenigvuldigen het aantal kolommen van de eerste matrix gelijk moet zijn aan het aantal rijen van de tweede matrix.
Het resultaat van een vermenigvuldiging van een 3x2 matrix met een 2x3 matrix is een 3x3 matrix. Om dat te onthouden kun je denken aan:
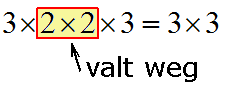
Het getal in de productmatrix dat op de tweede rij in de derde kolom staat is dus het product van de tweede rij van de eerste matrix en de derde kolom van de tweede matrix.
Heeft een matrixvermenigvuldiging betekenis?
Deze vraag is moeilijker te beantwoorden. De beste manier is om één van de getallen uit de productmatrix na te rekenen en dan precies na te gaan wat je nu eigenlijk doet.
Machten van een matrix
Een vierkante matrix met op de hoofddiagonaal uitsluitend enen en alle andere elementen gelijk aan nul heet een eenheidsmatrix.
Zo is $\left({\begin{array}{*{20}c}1&0&0\\0&1&0\\0&0&1\\\end{array}}\right)$ de 3x3-eenheidsmatrix
Je kunt een vierkante matrix met zichzelf vermenigvuldigen. In plaats van $A·A$ schrijven we $A^2$.
Je kunt met de GR (Run-Matrix-menu) met matrices rekenen. Dat neemt niet weg dat, om goed te begrijpen wat je aan het doen bent, je dat ook zonder GR moet kunnen.

|