3. matrices en kansen

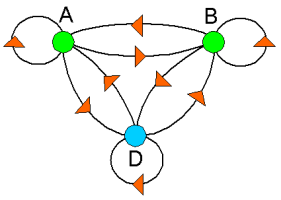
Overgangsmatrices Gegeven is een gerichte graaf met alle overgangen en de bijbehorende kansen in de overgangsmatrix $W$. $\begin{array}{*{20}c}{W=}&{\begin{array}{*{20}c}{van}\\{\begin{array}{*{20}c}A&{\,\,\,B}&{\,\,\,D}\\\end{array}}\\\end{array}}\\{\begin{array}{*{20}c}{naar}&{\begin{array}{*{20}c}A\\B\\D\\\end{array}}\\\end{array}}&{\left({\begin{array}{*{20}c}{0,6}&{0,2}&{0,2}\\{0,3}&{0,5}&{0,3}\\{0,1}&{0,3}&{0,5}\\\end{array}}\right)}\\\end{array}$ Geeft de matrix $W$ de kansen op de overgangen per dag dan geeft: de matrix $W^2$ die kansen per twee dagen de matrix $W^n$ de kansen per $n$ dagen

Markovketens Neem 's aan dat er in de graaf op deze pagina gaat om voedselplaatsen $A$ en $B$ en een drinkplaats $D$. In een bepaald gebied gaan de grazers van voedselplaats naar drinkplaats en andersom. De bijbehorende kansen per uur staan in onderstaande matrix. $\begin{array}{*{20}c}{W=}&{\begin{array}{*{20}c}{van}\\{\begin{array}{*{20}c}A&{\,\,\,B}&{\,\,\,D}\\\end{array}}\\\end{array}}\\{\begin{array}{*{20}c}{naar}&{\begin{array}{*{20}c}A\\B\\D\\\end{array}}\\\end{array}}&{\left({\begin{array}{*{20}c}{0,6}&{0,2}&{0,2}\\{0,3}&{0,5}&{0,3}\\{0,1}&{0,3}&{0,5}\\\end{array}}\right)}\\\end{array}$ Neem de kolommatrix met daarin het aantal dieren in de plaatsen $A$, $B$ en $D$. Met de matrixvermenigvuldiging $W·K$ kan je dan (bij gegeven kolommatrix) de aantallen uitrekenen na een uur. Naam aan $K=\left({\begin{array}{*{20}c}{160}\\{200}\\{240}\\\end{array}}\right)$. Om de aantallen na 1 uur te berekenen vermenigvuldig je $W$ met $K$. Je krijgt: $\left({\begin{array}{*{20}c}{0,6}&{0,2}&{0,2}\\{0,3}&{0,5}&{0,3}\\{0,1}&{0,3}&{0,5}\\\end{array}}\right)\cdot\left({\begin{array}{*{20}c}{160}\\{200}\\{240}\\\end{array}}\right)=\left({\begin{array}{*{20}c}{184}\\{220}\\{196}\\\end{array}}\right)$ Geeft de overgangsmatrix $W$ de kansen op de overgangen per tijdseenheid en de kolommatrix $K$ de verdeling op $t=0$ dan geeft $V^n·K$ de verdeling op $t=n$. Randvoorwaarden markovketen De in de matrix vermelde kansen blijven gelden Het aantal klanten, dieren, campers, e.d. blijft gelijk. Er is sprake van een gesloten systeem.

Markovketens en stabilisatie Een markovketen kun je gebruiken om voorspellingen te doen. Vaak (?) ontstaat er na verloop van tijd een evenwichtstoestand. Er treed stabilisatie op. Om de evenwichtstoestand te vinden kan je machten van $M$ berekenen. Ga door tot $M^n$ niet meer verandert. Als je de stabiele verdeling $K$ gevonden hebt kun je die eenvoudig controleren. Er moet gelden dat $M·K=K$. $\left({\begin{array}{*{20}c}{0,6}&{0,2}&{0,2}\\{0,3}&{0,5}&{0,3}\\{0,1}&{0,3}&{0,5}\\\end{array}}\right)\cdot\left({\begin{array}{*{20}c}{200}\\{225}\\{175}\\\end{array}}\right)=\left({\begin{array}{*{20}c}{200}\\{225}\\{175}\\\end{array}}\right)$ Lesliematrix Hier zie je een voorbeeld van een Lesliematrix: De blauwe getallen op de bovenste rij stellen de geboortecijfers voor (het gemiddeld aantal nakomelingen per individu). De rode cijfers (onder de hoofdiagonaal) stellen de overlevingskansen voor.

Populatievoorspellingsmatrices In een populatievoorspellingsmatrix staan in de eerste rij vruchtbaarheidscijfers. De overige elementen die niet nul zijn, zijn de overlevingskansen. Voorbeeld In een afgesloten ruimte houdt men een keversoort. Op een bepaal moment zijn er 400 eitjes, 200 larven en 50 kevers. Na één maand is 95% van de eitjes opgegeten of niet uitgekomen, het overige percentage heeft zich ontpopt tot larve. 75% van de larven heeft zich ontwikkeld tot kever. Elke kever heeft voor gemiddeld 100 eitjes gezorgd, maar van de oorspronkelijke kever is er niet één meer over. Vervolgens stellen we een overgangsmatrix op waarin we de verschillende overgangen verwerken: $\begin{array}{*{20}c}{}&{\begin{array}{*{20}c}{van}\\{\begin{array}{*{20}c}{eitje}&{larve}&{kever}\\\end{array}}\\\end{array}}\\{\begin{array}{*{20}c}{naar}&{\begin{array}{*{20}c}{eitje}\\{larve}\\{kever}\\\end{array}}\\\end{array}}&{\left({\begin{array}{*{20}c}0&0&{100}\\{0,05}&0&0\\0&{0,75}&0\\\end{array}}\right)}\\\end{array}$ Met behulp van matrixvermenigvuldiging kun je nu steeds de volgende generatie berekenen: $\left({\begin{array}{*{20}c}0&0&{100}\\{0,05}&0&0\\0&{0,75}&0\\\end{array}}\right)\cdot\left({\begin{array}{*{20}c}{400}\\{200}\\{50}\\\end{array}}\right)=\left({\begin{array}{*{20}c}{5000}\\{20}\\{150}\\\end{array}}\right)$ Herhaald toepassen levert het volgende verloop op: $\left({\begin{array}{*{20}c}{400}\\{200}\\{50}\\\end{array}}\right)\to\left({\begin{array}{*{20}c}{5000}\\{20}\\{150}\\\end{array}}\right)\to\left({\begin{array}{*{20}c}{15000}\\{250}\\{15}\\\end{array}}\right)\to...$ In dit soort gevallen kan er het volgende gebeuren: De populatie sterft uit De populatie vertoont een periodiek verloop De populatie neemt toe

• nog een voorbeeld

©2004-2024 W.v.Ravenstein