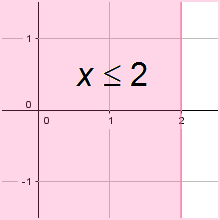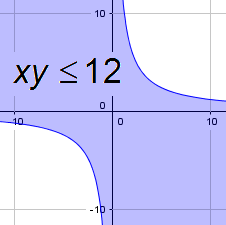|
Halfvlakken
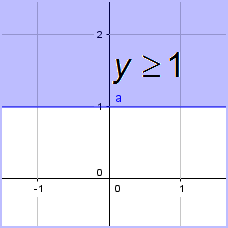
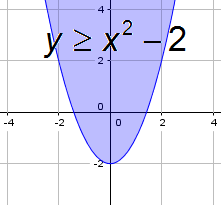
Een lijn verdeelt het vlak in twee halfvlakken.
De grafiek van $ax+by\le c$ is een halfvlak met rand begrensd door de lijn met vergelijking $ax+by=c$.
Voorbeeld 1
-
Teken het halfvlak met rand $2x-3y\ge 6$.
Uitwerking
Teken de lijn $2x-3y=6$. Deze lijn gaat door de punten $(0,-2)$ en $(3,0)$. Voor $(0,0)$ geldt $2·0-3·0\lt 6$, dus $(0,0)$ ligt niet in het gevraagde gebied. Je krijgt:
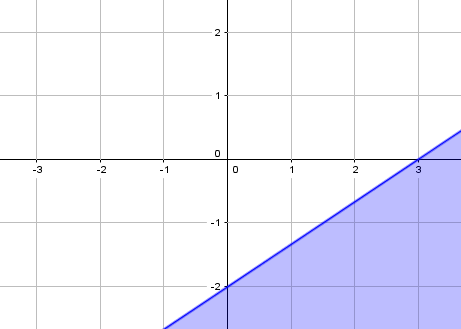
|
Begrensde gebieden
Een gebied kan ook begrend zijn door meerdere lijnen. Het gebied dat je moet hebben voldoet dan aan alle genoemde ongelijkheden.
Voorbeeld 2
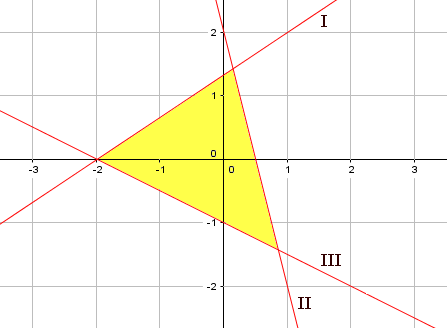
-
Schrijf de ongelijkheden op die bij dit gebied horen.
Uitwerking
Het gebied wordt begrensd door drie ongelijheden:
-
$2x-3y\ge-4$
-
$4x+y\le2$
-
$x+2y\ge-2$
|