de standaardvorm

Voor de standaardvorm  voor een wortelfunctie zou je dit voorschrift kunnen nemen:

• $f(x)=a+b\sqrt{c(x-d)}$

Je kunt het functievoorschrift opvatten als een ketting van transformaties die je uitvoert op de standaard wortelfunctie $y=\sqrt{x}$.

---

Transformaties

---

$f(x)=\sqrt{x}$

• vermenigvuldigen t.o.v. de y-as met de factor $
  \eqalign{\frac{1}{c}}
  $ geeft:

$f(x)=\sqrt{cx}$

• horizontale verplaatsing over de vector $
  \left( {\begin{array}{*{20}c}
     d  \\
     0  \\
  \end{array}} \right)
  $ geeft:

$f(x)=\sqrt{c(x-d)}$

• vermenigvuldigen t.o.v. de x-as met de factor $b$ geeft:

$f(x)=b\sqrt{c(x-d)}$

• verticale verplaatsing over de vector $
  \left( {\begin{array}{*{20}c}
     0  \\
     a  \\
  \end{array}} \right)
  $ geeft:

$f(x)=a+b\sqrt{c(x-d)}$

Tada!

---

Voorbeeld

---

$f(x)=2-3\sqrt{-2(x-1)}$ geeft:

a=2
b=-3
c=-2
d=1

---

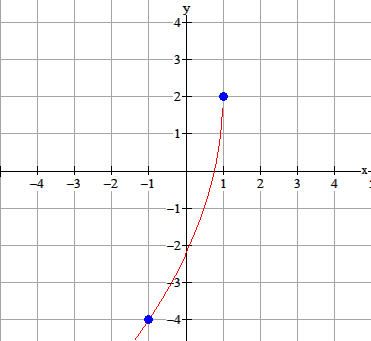
Controle

---

$
\begin{array}{l}
  - 2(x - 1) = 0 \\
 x - 1 = 0 \\
 x = 1 \\
 f(1) = 2 \\
 startpunt\,\,(1,2) \\
 ( - 1, - 4)\,\,invullen: \\
 f( - 1) = 2 - 3\sqrt { - 2\left( { - 1 - 1} \right)}  =  - 4 \\
 \end{array}
$
Klopt!

---

Toelichting

---

Je kunt aan het functievoorschrift in deze vorm het startpunt aflezen. Het startpunt is $(d,a)$. De waarden van $b$ en $c$ zijn iets lastiger:

• uitgewerkt met plaatjes

Je kunt overigens deze vorm gemakkelijk omwerken naar de 'oude vorm':

• $f(x)=a+b\sqrt{c(x-d)}$ wordt dan $f(x)=a+b\sqrt{cx-cd}$.

Andersom is het wel handig:

• Gegeven: $f(x)=5\sqrt{2x-6}-1$. Wat is het startpunt?
  Schijf $f$ als $f(x)=5\sqrt{2(x-3)}-1$ en je ziet het startpunt is $(3,-1)$.

Als je kijkt naar het startpunt en een roosterpunt dan kan je parameters aflezen uit de grafiek. Zie de uitwerkingen bij de oefening hieronder.

---

Oefeningen

---

Geef de waarden van $a$, $b$, $c$ en $d$ voor de standaardvorm $f(x)=a+b\sqrt{c(x-d)}$:

Opgave 1

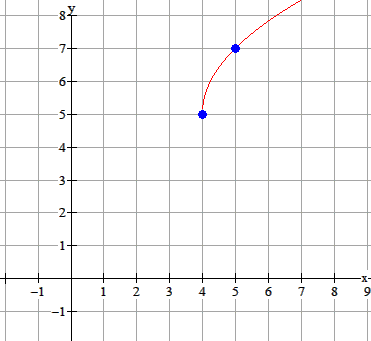
Opgave 2

• het functievoorschrift van het voorbeeld
• uitgewerkt met plaatjes
• uitwerkingen van de oefening

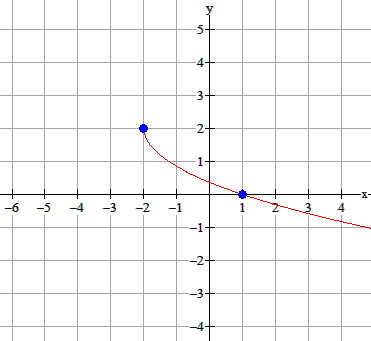
©2004-2024 W.v.Ravenstein