5. goniometrische vergelijkingen
Stel je voor dat je deze goniometrische vergelijking wil oplossen:
$\sin(\alpha)=\frac{1}{2}$
De vraag is dan wat is de waarde van $\alpha$ zodat de $\sin(\alpha)$ gelijk aan $\frac{1}{2}$ is.
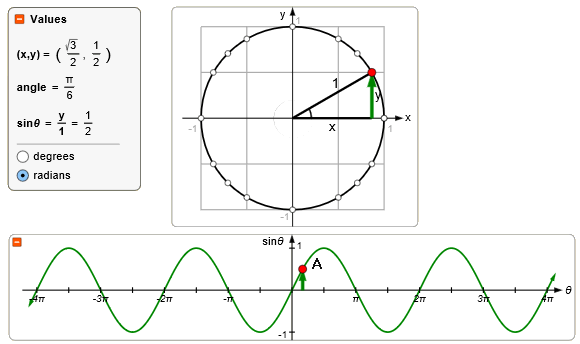
Je wist waarschijnlijk al dat de $\sin(30^o)$ gelijk is aan een $\frac{1}{2}$. In radialen is dat gelijk aan $\frac{1}{6}\pi$, dus je weet (in ieder geval) dat $\frac{1}{6}\pi$ een oplossing is.
In de grafiek is het punt $A(\frac{1}{6}\pi,\frac{1}{2})$ aangegeven...
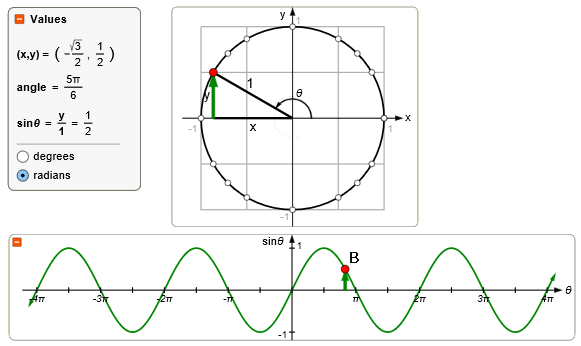
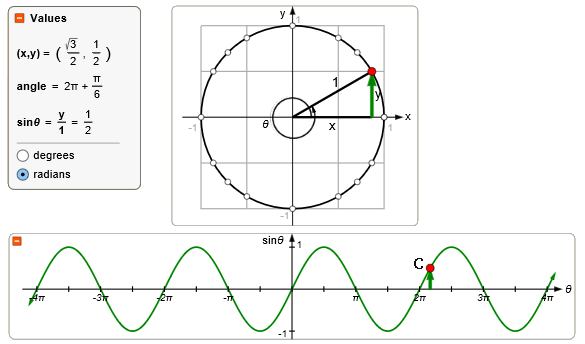
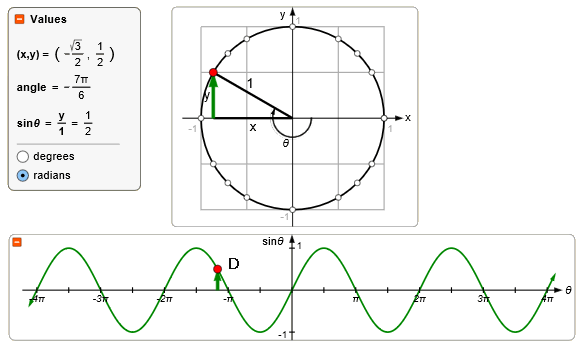
Maar er zijn nog veel meer hoeken die een sinus hebben gelijk aan een $\frac{1}{2}$. Punt B, C en zelfs D.
Kortom: er zijn oneindig veel oplossingen. Er zijn zelfs twee verschillende verzamelingen met een oneindig aantal oplossingen.
De vraag is nu: hoe kan je dat oneindig aantal oplossingen opschrijven en kan je er dan nog wel mee rekenen?
Voorbeeld
We gaan de vergelijking $2·\sin(3\alpha)+4=5$ oplossen
Stap 1
$
\eqalign{
& 2 \cdot \sin (3\alpha ) + 4 = 5 \cr
& 2 \cdot \sin (3\alpha ) = 1 \cr
& \sin (3\alpha ) = \frac{1}
{2} \cr}
$
Stap 2
We weten dat $\frac{1}{6}\pi$, maar dan ook $2\frac{1}{6}\pi$ en $4\frac{1}{6}\pi$, ... maar ook $-1\frac{5}{6}\pi$ en $-3\frac{5}{6}\pi$... allemaal een sinus van een $\frac{1}{2}$ hebben.
Je kunt dit kort opschrijven als:
$\frac{1}{6}\pi+k·2\pi$ met $k\in Z$.
Maar $\frac{5}{6}\pi$ was ook goed. Op dezelfde manier schrijf je dan:
$\frac{5}{6}\pi+k·2\pi$ met $k\in Z$
Stap 3:
$
\eqalign{
& 2 \cdot \sin (3\alpha ) + 4 = 5 \cr
& 2 \cdot \sin (3\alpha ) = 1 \cr
& \sin (3\alpha ) = \frac{1}
{2} \cr
& 3\alpha = \frac{1}
{6}\pi + k \cdot 2\pi \vee 3\alpha = \frac{5}
{6}\pi + k \cdot 2\pi \cr}
$
We zijn er bijna. Je moet nu nog links en rechts delen door 3. Bedenk daarbij dat je dan alle termen moet delen door 3...
Stap 4:
$
\eqalign{
& 2 \cdot \sin (3\alpha ) + 4 = 5 \cr
& 2 \cdot \sin (3\alpha ) = 1 \cr
& \sin (3\alpha ) = \frac{1}
{2} \cr
& 3\alpha = \frac{1}
{6}\pi + k \cdot 2\pi \vee 3\alpha = \frac{5}
{6}\pi + k \cdot 2\pi \cr
& \alpha = \frac{1}
{{18}}\pi + k \cdot \frac{2}
{3}\pi \vee \alpha = \frac{5}
{{18}}\pi + k \cdot \frac{2}
{3}\pi \cr}
$
Opgelost!