1. vermenigvuldigingsregel en somregel
Machtsbomen
Eén manier om handig te kunnen tellen is een boomdiagram.
Je gooit 3 keer met een euro (kop of munt). Hoeveel verschillende uitkomsten zijn er ?
De eerste keer kun je kop of munt gooien, de tweede keer ook en de derde keer ook, dus zijn er 8 mogelijkheden:
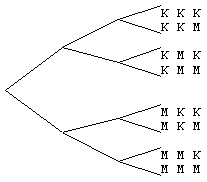Dit kun je aangeven met een boomdiagram, hierbij is naar boven 'kop' en naar beneden 'munt'. Uit elk punt van de boom vertrekken evenveel takken.
Faculteitsbomen
Soms vertrekken er van elk punt niet evenveel takken.
Bij een vereniging worden 3 mensen (A,B en C) in het bestuur gekozen die de functie van voorzitter, penningmeester en secretaris moeten vervullen. Op hoeveel manieren kan men deze 3 functies over deze 3 mensen verdelen?
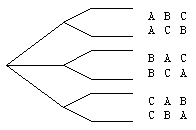Je krijgt nu een ander soort boom. Nu vertrekt er van elk punt steeds een lijn minder.
Je maakt hier de vermenigvuldiging:
3 x 2 x 1 = 6.
We noemen een boom als hierboven wel faculteitsboom.
Wegendiagrammen
In een wegendiagram worden wegen die naar één punt leiden samengevoegd.
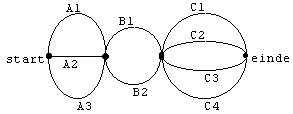
Hierboven staat een voorbeeld van een wegendiagram.
Op hoeveel manieren kun je van START naar EINDE ?
Er zijn in totaal 24 verschillende routes van start naar einde mogelijk.
Dit kun je uitrekenen door 3 x 2 x 4 = 24
Roosterdiagrammen
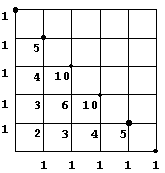
Als je bij een telprobleem steeds een keuze gemaakt moet worden uit twee alternatieven, dan ontstaat er een zeer regelmatig wegendiagram. We noemen zo'n wegendiagram een roosterdiagram. Het ziet er uit als roosterpapier.
Een gezin heeft 5 kinderen. Op hoeveel verschillende manieren kan het gezin zijn samengesteld?
Dit kan op 25 = 32 manieren.
Als je niet op de volgorde let, zijn er 6 verschillende samenstellingen mogelijk. Hierbij gebruik je de driehoek van Pascal.
