Rekenregels voor logartimen

Hoofdregel:
$
{}^g\log (x) = y \Leftrightarrow g^y = x
$

Hieruit volgt: $
g^{{}^g\log (x)} = x
$

Daarmee kan je de volgende regels aantonen:

$
\begin{array}{l}
{}^g\log (a) + {}^g\log (b) = {}^g\log (ab) \\
{}^g\log (a) - {}^g\log (b) = {}^g\log (\frac{a}{b}) \\
n \cdot {}^g\log (a) = {}^g\log (a^n ) \\
{}^g\log (a) = \large\frac{{{}\log (a)}}{{{}\log (g)}} \\
\end{array}
$
Voorbeeld:

$
\begin{array}{l}
5 + 3 \cdot {}^2\log (3) - {}^2\log (100) = \\
{}^2\log (2^5 ) + {}^2\log (3^3 ) - {}^2\log (100) = \\
{}^2\log \left( {\frac{{32 \cdot 27}}{{100}}} \right) = {}^2\log \left( {8\frac{{16}}{{25}}} \right) \\
\end{array}
$

Logaritmische vergelijkingen

Je kunt de rekenregels voor logaritmen gebruiken om logaritmische vergelijkingen op te lossen.

Voorbeeld

$
\begin{array}{l}
{}^2\log (x - 2) + {}^2\log (x) = 3 \\
{}^2\log (x(x - 2)) = 3 \\
x(x - 2) = 2^3 \\
x^2 - 2x = 8 \\
x^2 - 2x - 8 = 0 \\
(x + 2)(x - 4) = 0 \\
x =-2\,\,(v.n.)\,\,of\,\,x = 4 \\
x = 4 \\
\end{array}
$

• twee voorbeelden

---

Overgaan op een ander grondtal

Op de CASIO kan je met de functie logab logaritmen invoeren met een ander grondtal dan 10. Als je die functie niet hebt dan kan je gebruik maken van de volgende regel:

$\eqalign{{}^g\log (a) = \frac{{\log (a)}}{{\log (g)}}}$

Voorbeeld

$\eqalign{{}^2\log (12) = \frac{{\log (12)}}{{\log (2)}} \approx 3,584...}$

---

Logaritmen en de grafische rekenmachine

Denk bij het invoeren van je functievoorschriften aan de juiste vorm...GR?!

• Invoeren van logaritmische functies

---

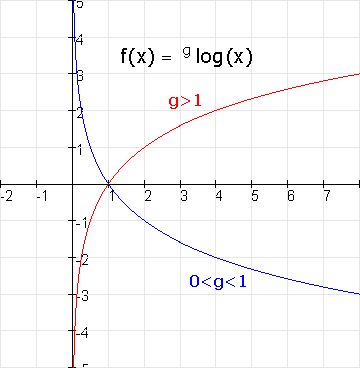
De logaritmische functie

$f(x)=\,^g\log{ax+b}$

Deze functies zijn standaardfuncties en de bijbehorende grafieken zijn standaardgrafieken.

Om het domein te berekenen van de functie $f(x)=\,^3\log{2x+5}$ los je de ongelijkheid $2x+5\gt0$ op. Je krijgt $x\gt-2\frac{1}{2}$ dus:

• ${D_f} =  <  - 2\frac{1}{2}, \to  > $

Uit het domein volgt dat de verticale asymptoot van de grafiek van $f$ de lijn $x=-2\frac{1}{2}$ is.

Afspraak

Bij het schetsen of tekenen van de grafiek van een logaritmische functie bereken je eerst het domein. Je tekent de verticale asymptoot als stippellijn in de figuur en zet de formule erbij.

---

---

Verdubbelingstijd en halveringstijd

De verdubbelingstijd bij exponentiële groei is de tijd waarin de hoeveelheid verdubbeld.

Bij groeifactor $g$ bereken je de verdubbelingstijd $T$ door de vergelijking $g^T=2$ op te lossen.

Bij exponentiële afname is de halveringstijd de tijd waarin de hoeveelheid gehalveerd wordt.

Bij groeifactor $g$ bereken je de halveringstijd $T$ door de vergelijking $g^T=\frac{1}{2}$ op te lossen.

---

Voorbeeld 1

Een hoeveelheid neemt jaarlijks met 13,1% toe.

• Bereken de verdubbelingstijd in maanden nauwkeurig.

Voorbeeld 2

Een hoeveelheid neemt wekelijks met 8,5% af.

• Bereken de halveringstijd in dagen nauwkeurig.

Zie uitwerking

---