3. transformaties en sinuso´de
Als je de hoek 'x' laat 'lopen' van 0° naar 180° en je tekent de grafiek van '$x\to sin x$' dan krijg je de grafiek van $f(x)=sin(x)$.
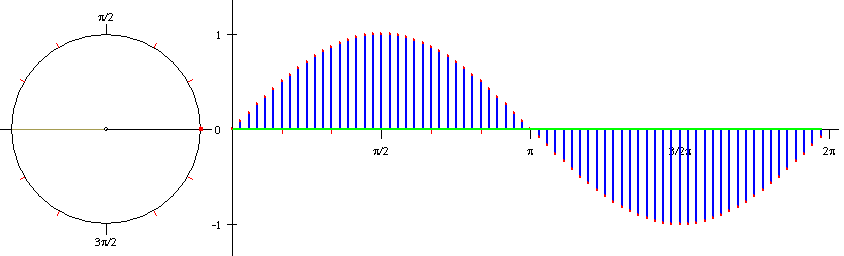
O, nee, x 'loopt' van 0 naar 2$\pi$:-)
We hebben nu de grafiek getekend van f(x)=sin(x). Zo kun je ook de grafiek van g(x)=cos(x) tekenen:
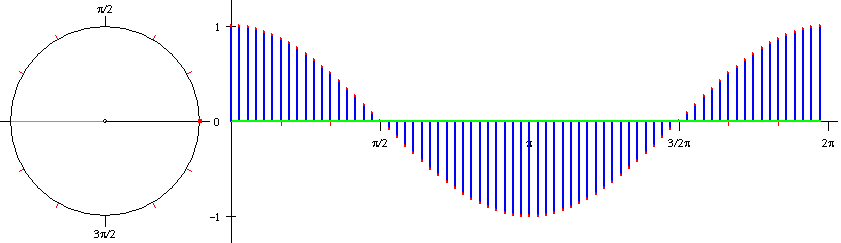
De grafiek van g(x)=cos(x) lijkt 'sprekend' op de grafiek van f(x)=sin(x). De grafiek van f is verschoven. Kennelijk is de grafiek van g(x)=cos(x) een transformatie van f(x)=sin(x). In deze paragraaf gaat het over transformaties van goniometrische functies.
Een transformatie is een afbeelding. Je kunt de grafiek van de sinus of cosinus ook verschuiven, spiegelen of vermenigvuldigen. Als je de grafiek van een sinusoide transformeert dan verandert ook het functievoorschrift. De 'kunst' is om 'transformaties' te koppelen aan de wijzigingen van het functievoorschrift.
Zie overzicht transformaties van grafieken 2 voor een overzicht van de transformaties die we in dit hoofdstuk nodig hebben. Hieronder zie je de voorbeelden en een aantal toetsopgaven.
- 1. horizontale verschuiving
- 2. verticale verschuiving
- 3. spiegelen in de x-as
- 4. spiegelen in de y-as
- 5. vermenigvuldigen t.o.v. de x-as
- 6. vermenigvuldigen t.o.v. de y-as
- 7. toetsopgaven als voorbeelden