4. gelijkvormigheid driehoeken
Gelijke hoeken zoeken
Om gelijkvormigheid van driehoeken aan te tonen heb je twee paar gelijke hoeken nodig. Bij het opsporen van gelijke hoeken gebruik je de volgende eigenschappen:
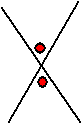
Bij snijdende lijnen zijn de overstaande hoeken gelijk:
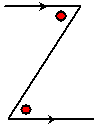
Bij evenwijdige lijnen horen gelijke Z-hoeken:
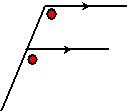
Bij evenwijdige lijnen horen gelijke F-hoeken:
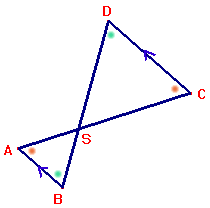
$\Delta ABS \sim \Delta CDS$
Lengte x stellen
Soms is het handig de lengte van een lijstuk $x$ te stellen. Door vervolgens de lengte van het overeenkomstige lijnstuk uit te drukken in $x$ kun je door kruislings vermenigvuldigen $x$ berekenen.
Voorbeeld
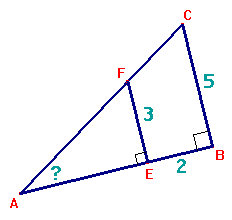
Gegeven: $BC=5$, $EF=3$ en $EB=2$.
Gevraagd: Bereken de lengte van $AE$.
- Zie uitwerking
Ruimtefiguren (wiskunde B)
Soms kun je bij het berekenen van de lengte van een lijnstuk in een ruimtefiguur gebruik maken van gelijkvormige driehoeken.
Het is handig om de gelijkvormige driehoeken uit de figuur te lichten en deze apart te tekenen.
Voorbeeld
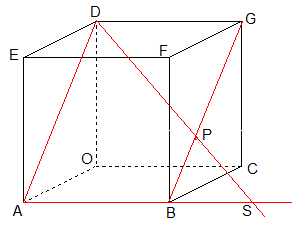
Gegeven een kubus met zijde 8. Op het lijnstuk BG ligt het punt P zodat BP=$2\sqrt{2}$. De lijn DP snijdt AB in het punt S.
- Bereken de lengte van BS.
Uitwerking
Ga na dat $\Delta ASD \sim \Delta BSP$. Neem $BS=x$. Ga na dat geldt:
$
\eqalign{{{8 + x} \over x} = {{8\sqrt 2 } \over {2\sqrt 2 }}}
$
Oplossen geeft je waarde van $x$.
$
\eqalign{
& {{8 + x} \over x} = {{8\sqrt 2 } \over {2\sqrt 2 }} \cr
& {{8 + x} \over x} = 4 \cr
& 4x = 8 + x \cr
& 3x = 8 \cr
& x = 2{2 \over 3} \cr}
$
$BS=2\frac{2}{3}$