` Wiskundeleraar
©2012 wiskundeleraar.nl

4. logaritmen

De logaritme

In $^glog(x)$ heet $g$ het grondtal van de logaritme.

$^glog(x)$ is de exponent van het grondtal $g$ waarmee de macht gelijk is aan $x$.

$g^{^glog(x)}=x$

Hoofdregel

Als $^glog(x)=y$ dan $x=g^y$

Voorbeelden

  • $^2log(\frac{1}{8}\sqrt{2})=-2\frac{1}{2}$
  • $^5log(0,04)=-2$

Logaritmische vergelijkingen

  • Als $^glog(x)=y$ dan $x=g^y$

Voorbeeld

$
\eqalign{
  & a.\,\,\,{}^3\log \left( {2x^2  - 3} \right) = 6  \cr
  & b.\,\,\,{}^{\frac{1}
{2}}\log \left( {\frac{1}
{{4x}}} \right) = 4  \cr
  & c.\,\,\,{}^2\log \left( {4 - 30x^2 } \right) =  - 2 \cr}
$

Zie logaritmische vergelijkingen uitgewerkt

Logaritmische functie

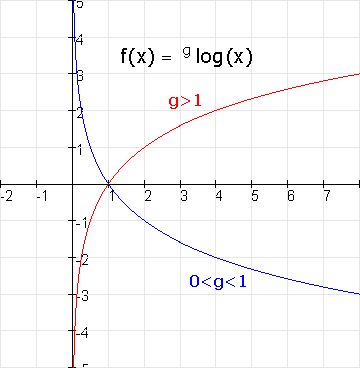
De functie $f(x)=^glog(x)$ is een standaardfunctie. De grafiek is een standaardgrafiek.

  • domein:$<0,\to>$
  • stijgend voor g$>$1 en dalend voor 0$<$g$<$1
  • bereik $R$
  • verticale asymptoot x=0

De vergelijking ax=c

De exacte oplossing van de vergelijking $a^x=c$ is $x=^alog(c)$

Voorbeelden

Bereken de exacte oplossing van:

  • $3^{x+1}=80$
  • $5+2^{3x}=25$
  • $\eqalign{4-log(\frac{1}{x})=2}$

Zie logaritmische vergelijkingen deel 2

Je kunt grafieken van functies van de vorm $f(x)=^glog(ax+b)+c$ opvatten als een combinatie van transformaties van de standaardfunctie.


Variabelen vrijmaken bij exponentiële formules

Hier gaat het er om dat je een formule als bijvoorbeeld y=500-100,1x+1,5 ook kan schrijven als x=.... We noemen dat 'x vrijmaken'.

Voorbeeld

$
\eqalign{
& y = 500 - 10^{0,1x + 1,5} \cr
& 10^{0,1x + 1,5} = 500 - y \cr
& 0,1x + 1,5 = \log (500 - y) \cr
& 0,1x = \log (500 - y) - 1,5 \cr
& x = 10 \cdot \log (500 - y) - 15 \cr}
$

Nog een voorbeeld

$
\eqalign{
& y = 2 \cdot 3^x + 1 \cr
& 2 \cdot 3^x = y - 1 \cr
& 3^x = \frac{{y - 1}}
{2} \cr
& x = {}^3\log \left( {\frac{{y - 1}}
{2}} \right) \cr}
$

Extra opgaven:

Maak $x$ vrij:

  • $y=25-5^{\frac{1}{2}x+2}$
  • $y=3\cdot2^{x}+5$
  • $y=10^{x^{2}}-1$

Zie extra opgaven uitgewerkt

Home Vorige

Terug Home

Login View